自然言語処理

私たちが日常的に使っている「言葉」は、感情を伝えたり情報を整理したりするための重要な手段です。こうした人間の言語をコンピュータで処理する技術を「自然言語処理」と呼びます。言語にはあいまいさや文脈の理解といった独特の難しさがあり、これらを数式やデータとしてどのように扱うかがこの分野の面白さです。
自然言語処理は、文の構造や意味の理解といった基礎技術に加えて、検索エンジン、機械翻訳、音声アシスタント、対話システムなど、私たちの生活に身近な技術に広く応用されています。また、近年急速に発展している生成AIも、大量の言語データをもとに学習する「大規模言語モデル(LLM)」に基づいており、自然言語処理の研究成果が活かされています。
本講義では、言語の構造や意味をデータとしてとらえるための基本概念と手法を学び、さらに自然言語処理の代表的な応用例を通じて、AI技術とのつながりや社会への影響についても理解を深めます。
電気電子材料学
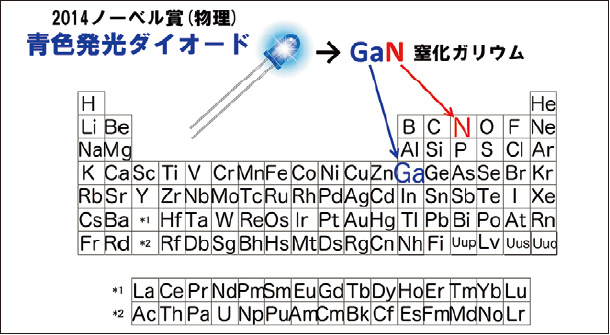
「物質」とは私たちの身の回りにある固体・液体・気体などのことです。何かに応用される物質のことを「材料」と呼びます。あらゆる材料は周期表にある118個の原子単体またはその組み合わせから原理的につくり出すことができ、用途に応じて分類され、工業材料、生体材料、ナノ材料、複合材料などがあります。
電気電子材料とは抵抗、コンデンサ、ダイオード、トランジスタなどの回路素子を構成する金属・半導体・絶縁体・磁性体材料のことです。これらの材料が持つ電気磁気的な性質は構成原子中に存在する電子の性質によって決まります。材料中電子の性質を解明し、その制御技術を確立して応用へと結びつけることで、現代計算機社会に不可欠なパソコンやスマートフォンなどの便利な製品が生み出されてきました。
本講義では、さまざまな回路素子の構成原子、その結晶構造と電子のエネルギー構造を知り、これらの特徴と素子の持つ機能との関係を理解することで、新しい性質を持つ電気電子材料をつくるための基礎を築きます。
応用数学Ⅰ
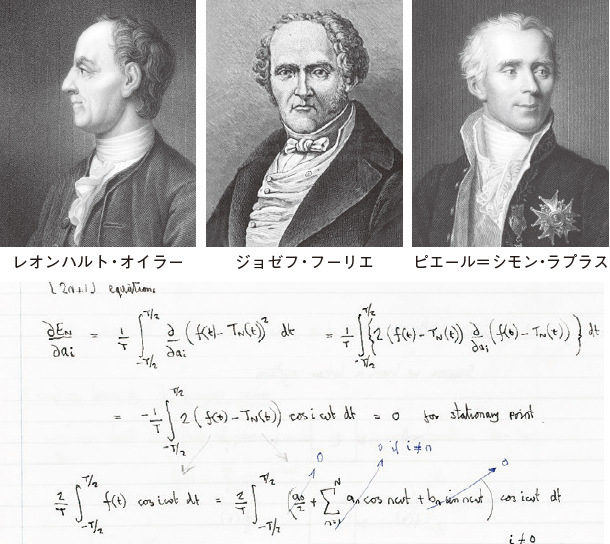
オイラー、フーリエ、ラプラス、これらのヨーロッパの数学者の名前は工学の応用と切っても切れない関係にあります。彼らのおかげで指数関数と三角関数は結びつき、周期関数は様々な要素に分解され、微積分方程式を便利に解くことができるようになりました。
応用数学Ⅰという科目では、電子情報工学の応用に役立つこれらの事柄を身につけることを目標とします。道具としてただ使えるだけでなく、なぜ使えるのかという部分を理解することが大事です。
数々の大数学者が感じたであろうロマンに思いを馳せ、それを少しでも楽しんでもらえれば、より良い理解につながると思われます。



